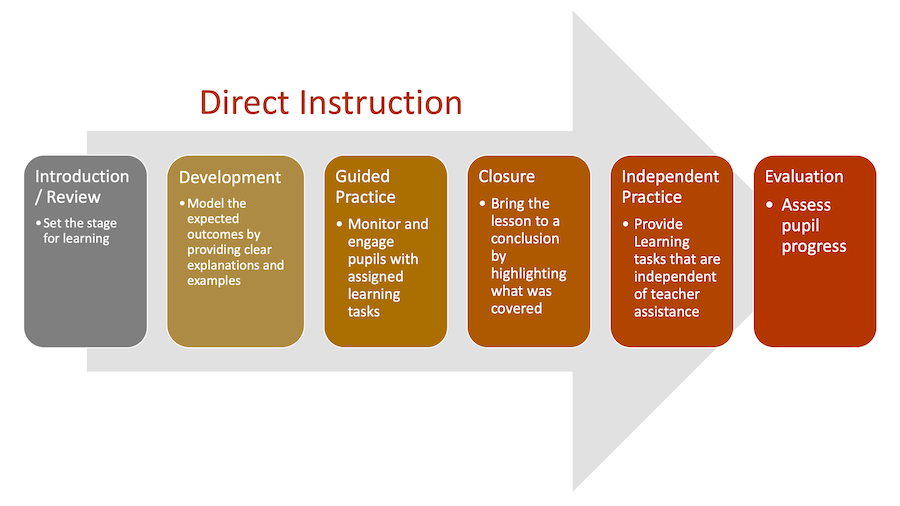
Direct instruction was a specific model developed by Siegfried Engelmann and Wesley C. Becker. It is a teaching technique that emphasizes well-planned and well-developed sessions centered on tiny learning increments and clearly defined and regulated teaching activities.
There are five key philosophical principles:
- All children can be taught.
- All children can improve academically and in terms of self image.
- All teachers can succeed if provided with adequate training and materials.
- Low performers and disadvantaged learners must be taught at a faster rate than typically occurs if they are to catch up to their higher-performing peers.
- All details of instruction must be controlled to minimize the chance of students’ misinterpreting the information being taught and to maximize the reinforcing effect of instruction.
This technique is widely used in a plenty of schools around the world. It is the most common method that teachers use in class, as we familiar, teachers review knowledge we know first, next, introduce tiny new knowledge, then we will practice this new knowledge and teacher will give us feedback to make sure we understand it. I have been taught in this mode for almost my whole school life. Based on my experience of learning in direct instruction approach, it is very helpful in science courses, especially mathematics.
Since the topic we chosen in our group is to teach how to solve linear function and quadratic function in math, direct instruction aligns our topic well. We review how to solve equations with one variable first, on the basis of this, we introduce linear function and quadratic function. Next step, we get into it through learning how to solve linear function and quadratic function and how to graph them. At last, practice questions are given to train learners skills. The learning outcomes will be assessed by quiz and exam.
Cox, C. (n.d.). Basic philosophy of direct instruction (DI). Retrieved from https://www.nifdi.org/15/index.phpoption=com_content&view=article&id=52&Itemid=27
This is a good method that we can use in our learning pot. Through direct teaching, we can know students’ levels in our learning pot, and we can develop an exclusive learning assessment plan for each student. One of the key philosophical principles that can support we help learners to be confident with their math level. At the same time, we can quickly know the progress of students in the learning pot.
Here is my teammate’s blog and my comment:
https://haiyangma.opened.ca/blog-2/